ICPC训练赛-Philosopher‘s Walk

题意

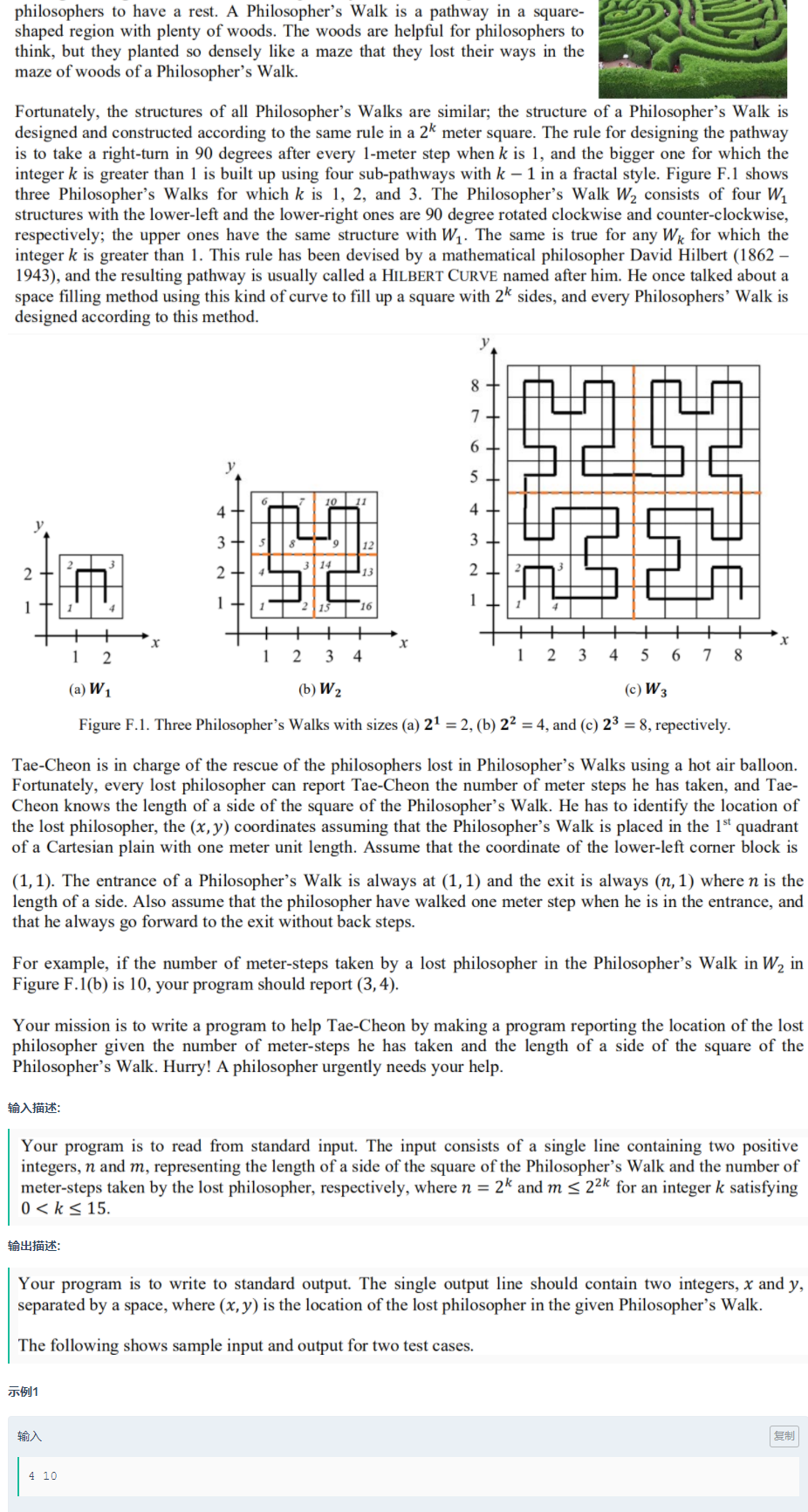
image-20210415121210364

image-20210415121231522

如图所示，给定这样的一个n阶图形，每次从左下角开始走，问走了m步后的位置坐标？

这个图是有规律可循的，定义f(i)是i阶图的样子，那么f(i+1)就是四个f(i)拼成的，上面两个和f(i)一样，左下角是f(i)顺时针旋转90度得到，右下角是f(i)逆时针旋转90度得到，因此可以定一个dfs函数返回的是坐标，不管这个图形是否旋转，我们只求这个图形没有旋转，也就是正着放时走m步的坐标，即使它旋转了，这个坐标也只不过是换了一个角度而已，我们是知道图形的尺寸的，那就可以根据这个尺寸来推出这个点的坐标

CODE

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N=100010;
int n,m; 
pii dfs(int x){
	if(x==1) return {1,1};  //一阶方阵直接返回坐标(1,1)
	x/=2;  
	int res=x*x;  //算出1/4的尺寸有多少个小方格
	if(m>3*res){  //如果在第4个子图内
		m-=3*res;  //减一下步数
		pii tmp=dfs(x);  //得到在这个小子图(正着放)左下角开始跑m步的坐标
		return {x*2-tmp.second+1,x-tmp.first+1};  //核心，尽管跑出来的是正着放的坐标，但是可以转化为在当前图形的坐标
	}
	else if(m>2*res){
		m-=2*res;
		pii tmp=dfs(x);
		return {x+tmp.first,x+tmp.second};
	}
	else if(m>res){
		m-=res;
		pii tmp=dfs(x);
		return {tmp.first,x+tmp.second};
	}
	else{
		pii tmp=dfs(x);
		return {tmp.second,tmp.first};
	}
}
int main(){
    cin>>n>>m;
    pii ans=dfs(n);
    cout<<ans.first<<' '<<ans.second<<'\n';
    return 0;
}