题目链接
题目描述
题目大意:
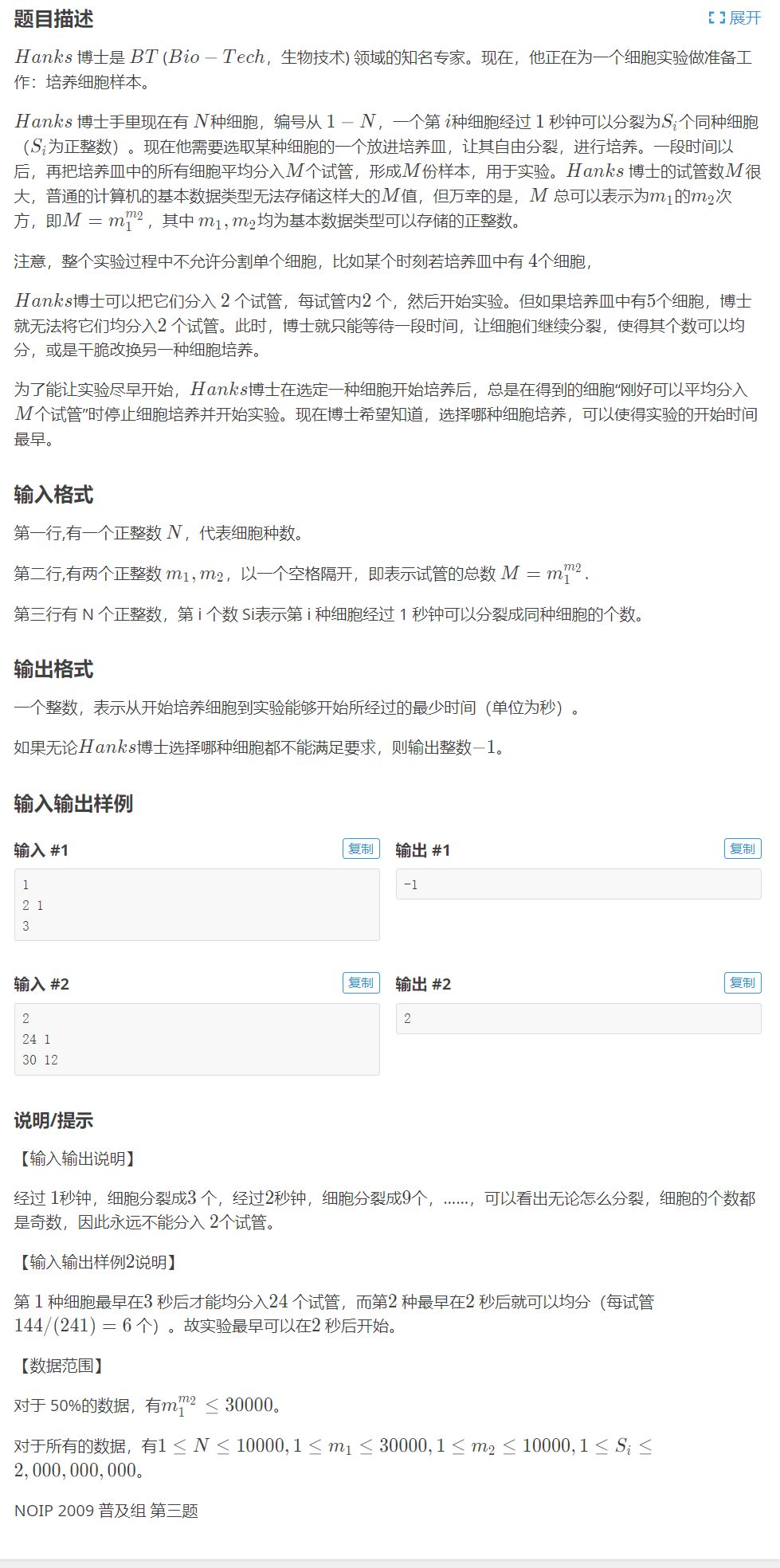
有n种不同数量的细胞,每一个细胞每一秒都会分裂出一个新的,现在要把某一种细胞平均分到m1^m2^个容器里面,问选一种细胞,使得等待的时间最短,如果无法均分到容器中,就输出-1
做法
要均分就表示Si^t^%m1^m2^==0求t的最小值,看一下数据范围发现m1比较小,而Si很大,分别对Si和m1分解质因子,只要m1中的每一个质因子Si中都有,那么Si就可以通过分裂均分到m1^m2^中,因此不需要把Si的所有质因子都找到,只需要找到小于等于m1的所有质因子即可,因此时间复杂度就是n*3e3就是3e7,对于m1和Si共有的质因子需要满足pi*t>=pm1*m2,要让满足条件的t最小就是取所有共有质因子的最大比值,然后所有比值中取最小
CODE
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include <bits/stdc++.h>
#define debug freopen("in.txt","r",stdin); freopen("out.txt","w",stdout)
#define ios ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int MAXN=1e6+100;
const double pi=acos(-1);
const int MOD=1e9+7;
const int INF=0x3f3f3f3f;
const int SUB=-0x3f3f3f3f;
const int eps=1e-4;
int tail,pr[MAXN/10];
bool np[MAXN];
void ol(){
np[1]=1;
for(int i=2;i<=1000000;i++){
if(!np[i]) pr[++tail]=i;
for(int j=1;j<=tail && pr[j]<=1000000/i;j++){
np[i*pr[j]]=1;
if(i%pr[j]==0) break;
}
}
}
int n,m1,m2;
int S[MAXN],z1[MAXN],z2[MAXN];
int main(){
ios;
ol();
cin>>n>>m1>>m2;
for(int i=1;i<=n;i++) cin>>S[i];
if(m1==1){
cout<<0<<'\n';
return 0;
}
for(int i=1;i<=tail && pr[i]<=m1/pr[i];i++){
while(m1%pr[i]==0){
z1[pr[i]]+=m2;
m1/=pr[i];
}
}
if(m1>1) z1[m1]+=m2;
int ans=INF;
for(int i=1;i<=n;i++){
memset(z2,0,sizeof z2);
int bk=S[i];
for(int j=1;j<=tail && pr[j]<=S[i]/pr[j];j++){
while(S[i]%pr[j]==0){
z2[pr[j]]++;
S[i]/=pr[j];
}
}
if(S[i]>1 && S[i]<=30000) z2[S[i]]++;
int flag=0,mx=-1;
for(int j=1;j<=tail;j++){
if(z1[pr[j]] && !z2[pr[j]]){
flag=1;
break;
}
else if(z1[pr[j]] && z2[pr[j]]) mx=max(mx,(z1[pr[j]]-1)/z2[pr[j]]+1);
}
if(!flag) ans=min(ans,mx);
}
if(ans!=INF) cout<<ans<<'\n';
else cout<<-1<<'\n';
return 0;
}
|


